There's a nerd in my elevator!

This text appeared first in Naukas, where was originally written in Spanish.

Recently I started a secondment at the Friedrich Schiller University, in Jena, Germany. Surprisingly, my office during the next months is located in the 18th floor of a skyscraper. The Jentower in particular:

But I'm not writing this to boast about the views of my new office. On the contrary, I'll destroy any possible idea of glamour related to work in a place like this. And I'll do it with a confession: I became the crazy guy who leaves his cell phone on the ground while he uses the elevator. Let me explain:

A building of almost 150 meters high needs fast elevators. The ones in this building have a very powerful, scary acceleration. Then, I remembered that smartphones usually contain an accelerometer, so I tried to measure those accelerations.

I used an app called Google Science Journal, that allows registering data from all sensors available in the phone (accelerometers, light, magnetic field, ...) and export them in a format (.csv) quite easy to analyze on a computer. If you like getting your hands dirty, install it now!

In the figure below we can see the vertical acceleration profile during my trip to the 18th floor this morning, where we can clearly see the initial "kick" (seconds 9 to 14) and the braking (28 to 33)

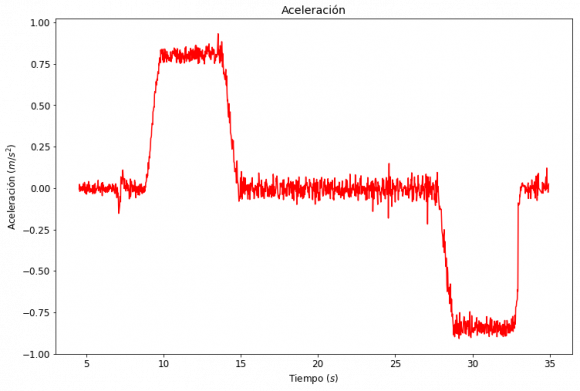Vertical acceleration (excluding gravity)

Accelerations of 1 m/s^2 sustained during 4 seconds! You can feel that in your stomach!

Using this data, we can explore a bit further. We can use a time series of the acceleration to compute speed and position. How? Maybe you remember from high school's physics that position, speed and acceleration are related through derivatives. More specifically.

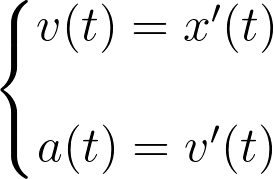
With the previous recipe we can compute speed using the position, and then use speed to compute acceleration. Like in a production chain. Nevertheless, in our case we want to do the opposite process. Luckily, we can use indefinite integrals to "revert" our derivatives, and thus our whole "production chain".

So, by integrating the acceleration (to obtain the speed), and then integrating the speed (to obtain the position) we find results like this:

Acceleration, speed and position

So, using only a device that most of us carry everywhere and some elementary physical concepts we know that:

• Our elevator runs up at 4 m/s.
• My office is 74 meter above the ground.

Such a great time to be a nerd!

If someone is interested in exploring a bit deeper into the details (for instance: how to filter out the effects of gravity, how to integrate a time series, ... ) or even experiment with his or her own elevator, here is a link to the code I've used.