Visualization of a 3D Levi-Civita symbol

The Levi-Civita symbol is that puzzling \(\epsilon_{ijk}\) term that appears in the calculation of determinants and vector products. It has, thus, lots of applications in algebra, geometry, mechanics, electromagnetism, ... A (boring) definition is given in the textbox below.

---

The value of \(\epsilon_{ijk}\) goes as follows:

It is \(0\) if the value of any index is repeated, such as in \(ijk = 112\)

It is \(1\) if the indices are \(ijk \in123, 312, 231\)

It is \(-1\) if the indices are \(ijk \in 321, 132, 213\)

---

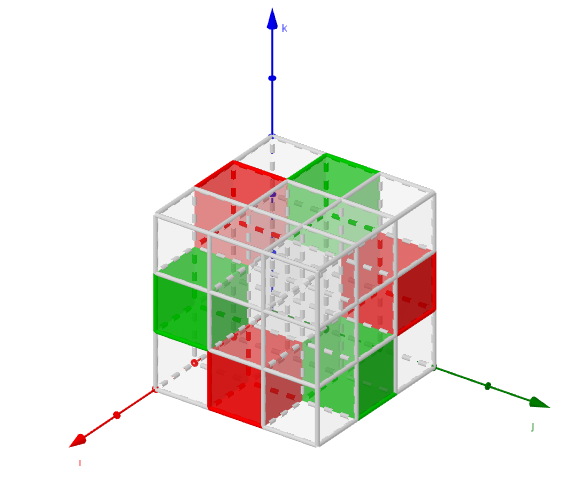
I am interested in visualization. Unfortunately, the Levi-Civita symbol has three indices, \(i\), \(j\) and \(k\), so we cannot represent it as a matrix or a vector. But, taking advantage of its discrete nature (it can only take 3 different values) we can create a "cubic matrix" to visualize it. This matrix contains \(3 \times 3 \times 3\) cubes, each of them univocally identified by a triplet \(ijk\), and the color tells us its value (grey for \(0\), green for \(1\), red for \(-1\)).

That's what I did in a GeoGebra applet. I leave it here, just in case anyone finds it interesting. Click on the image to open an interactive version where the cube can be rotated.